그럼 출발~~~!!!

요고이 이번에 해볼 도면이다. 응? 극악샒~ 이거 수치가 틀린뎁셔?? 라고 질문하지 마라... 매번 수치로 난장까는 도면이 나오겠지만....
결국은 같은 사이즈란거 기억해 두기 바란다. 반지름 값이 변해도 결국 너희들에게 주어질 Bender는 결국 안지름 32mm짤~~ 이니까 ㅋㅋㅋ
그리고 길이는 끝부분에서 장난질 하거나 아니면 이번처럼 바깥쪽에서 시작해서 안쪽으로 끝나거나,, 아님 중심선에서 시작해서 중심선이던...
아님 안쪽에서 안쪽이겠지... 그렇게 길이로 장난질 하는거니 헷갈리지 말고 이 도면을 기준으로 계산을 빨리하는 방법을 택하는 것이 좋겠다.
물론 자신이 1:1 Scale의 도면을 먼저 그리고 그에 맞게 구부리는게 장땡~~!! ㅋㅋㅋ
가자.... 일단 구분을 지어서 부분적으로 길이를 재서 나가는 것이 좋겠다. 응? 왜??
그건 내맘이다... 억울함 니~~맘대로 하세요 ㅋㅋㅋ

제군들 보이나... 이건 1:1 Scale로 만든 그림이다.
하지만 포스팅이다 보니 당연 그림이 실제보다 작아질 수 밖에 없었다. 이점 이해하기 바란다 ㅋㅋ(실제로 A2 용지에 꽉찬다 ㅋㅋ)
일단 지름 12mm짤 알루미늄 튜브란건 제군들이 더 잘 알끼다.. 그럼 반지름이 6mm란 소리겠지....
먼저 A구간의 길이를 구해보자... 겁나게 쉽다. 오른쪽에 튜브의 끝단부터 90도 구부러진 끝단(외경)까지 140mm라고 찍혀 있군.
그럼 A구간은 140에서 뭘 빼야 할까???? 당근을 뺄까? (정말 당근이라 생각한다면 일단 맞고보자 ㅋㅋ)
웃기지 마라 이제부턴 계산기와 친해져야한다.... 물론 이건 간단한 거니 암산으로 가능~~
핑크색의 원들이 보이는가? 가장 안쪽의 반지름은 32mm이다. 중심선의 반지름은 38mm이고 그럼 가장 바깥의 반지름은??
뭘 생각하냐? 가뿐하게 6mm를 더해준 44mm이다. 핑크색의 원은 제군들이 사용할 튜브벤더용 Tool이라 생각하면 편할게다.
가장 바깥원을 기준으로 140mm를 찍었으니 이건 튜브의 외경까지를 포함한다 보면 된다. 반지름은 어느 각도에서도 길이가 변하지 않는다.
90도가 되어도 34도가 되어도 반지름은 영원히 같으니 가장 바깥의 반지름 44를 빼주면 되겠다.
A = 140 - 44 = 96mm
하하하하하...... 쉽지 않은가? A구간의 길이 96이 나왔으니 그 부위에 표시해주고 벤더에 물려서 가뿐히 90도 구부려 주자.
짭... 그렇다고 딱 90까지 구부리면 안되는거 다들 알지? 재질 원래의 탄성 때문에 조금 더 구부려야 한다. 아님 90도가 아닌 88이나 87도가 나오니까
각도를 더 넘기는건 제군들의 재주에 맏기겠다. ㅋㅋㅋㅋㅋ
아차.. 가끔 도면에 외경이 아닌 중심선 까지의 길이로 표현 하는 경우가 있다. 그럼 140mm가 중심선 까지라면 제군들은 얼마를 빼겠는가?
당근 빠따~~~!! 140mm에서 38mm를 빼주면 된다. 헷갈리지 마라. 140mm가 어디 까지의 길이인지가 중요한 게다. ㅋㅋ
B구간 길이는.... 뭘 물어보나... 당근 44mm이지 않는가? 왜? 140mm의 끝이 외경에 닿아 있기 때문이지 ㅋㅋㅋ
응?? 근데 여기서 또 알고 싶은게 있다... 뭘까?? 그럼 이 튜브를 구부렸을 때 기럭지는 얼마일까? 곡선이라 모르겠다?? 설마 ㅋㅋㅋ
중심선을 기준으로 원호를 구해보면 기럭지가 짠하고 나온다. 응? 원호의 길이는 어떻게 구하냐구? 제길...슨...
그래 그럼 원호의 길이를 구하는 식을 알아보자.
파이... 초코파이... 엄마손 파이.... 빅파이....... 응?? 뭐 이건 아니고 ㅋㅋ
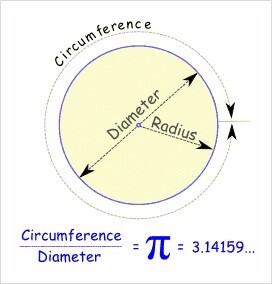
원주율이 파이란다. 파이...?? 귀에 못이 박히게 들었을법 한 녀석이다 3.141592....... 무한대로 나가는 이녀석 ㅋㅋ
Diameter는 지름이고 Radius는 반지름이다. 보통 원의 둘레를 구하는 것은 원주율 X 지름.... 되시겠다.
고로 내가 그려 놓은 핑크색 원들 중에 중간에 있는 38mm짤 원의 둘레는 3.14 X 38 X 2 = 238.64......로 나오신다.
근데 우리는 90도라는 각도를 갖고 있는 4등분 된 원이 아니던가~~~ 그럼 나누기 4....하면... 59.66....라고 나오는데.... 응??
근데.. 우리에게 알려준 것은 반지름... ?? 그럼 원의 둘레는...
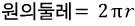
거기다 우리는 90도라는 각도까지 있다.. 물론 90도면 4분의 1이니 4로 나누면 되겠지만 37도 49도... 이런거 어쩔~ ㅋㅋㅋㅋ
그래서 여기에 각도를 넣어 주면 쉽게 계산이 된다.
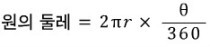
그럼 우리가 첫번째 구부린 90도를 계산해 보면
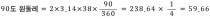
요로케 나오게 된다. 훔훔... 근데 극악샒~ 도면과 수치가 틀린뎁쇼...??
그러게 ㅋㅋㅋ 하지만 착각하지 마라 ~!! 쉽게 계산하기 위해 3.141592.........로 나가는 것을 확 쭐여서 3.14로 계산해서 그런거다.
그리고 캐드는 이런거 안 빗겨 나간다. ㅋㅋㅋ 계산이 확실하지....ㅋㅋㅋㅋ
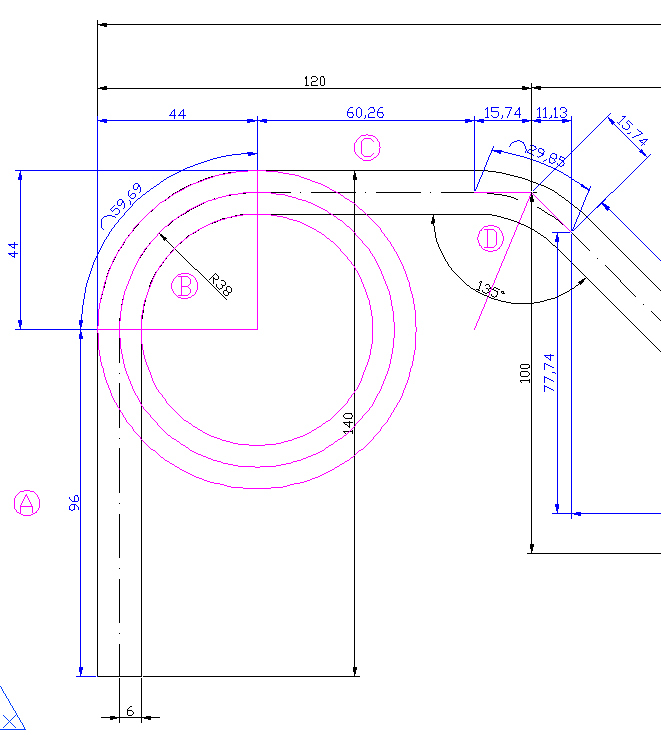
이번엔 C를 구해보자. 응? 근데 이거...... 양쪽의 길이를 빼야 하네....
뭐 일단 구해서 빼면 되는 것이니 구하는 방법을 알아보자....
일단 90도 꺽은 부위 포함해서 다음 꺽이는 중심점까지의 거리를 120mm로 놓았다.
근데... 우리는 90도 꺽고 다음에 얼마를 남기고 구부려야 할지 모른다... 이게 문제다...
B구간의 길이 44mm를 이미 알고 있으니.... 120에서 B구간을 빼면 76mm가 남는다.
근데.. 이게 다가 아니다. 일명 SET BACK이란 거리만큼 또 빼줘야 하는 것이다.
응?? 근데 SET BACK이 뭐야??
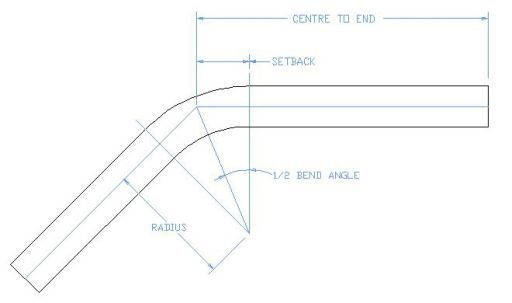
SET BACK은 굽힘이 시작되는 부분부터 굽힘점 까지의 길이를 말하는데.. 그림처럼
중심점의 연장선을 그려서 서로 교차되는 부위까지의 거리를 세트백... 이라고 한다. 결국 직선으로 연장된 선의 길이를 말하는 거다.
근데 이게 왜 필요해...?? 그러게 ㅋㅋㅋ
근데 모르면 말이다. 구부러진 부분의 직선 거리를 알지 못하게 된단다. 그럼 수평거리에서 곡선이 갖고 있는 직선거리를 모르게 된다는 거지.
문제는 전체의 길이를 구부러지던 직선이던 사선이던 몽짱 수평직선으로 표시했다는게 중요하다.
응? 근데 저기엔 대각선은 왜 있냐구?? 그럼 피타고라스랑 친해지거라 ㅋㅋㅋ 그럼 대각선을 갖고 직선을 구할수 있을게야 ~~
일단 SET BACK을 구하는 식을 알아보자.. 알아야 길이를 구하지 ㅋㅋ
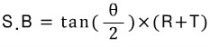
오호~ 이거 봐도 모르겠다...?? sin, cos, tan, 이거 어디서 많이 본거 같지 않냐?? ㅋㅋ
S.B는 Set Back의 약어이고 Θ는 그림에 나온 각도를 넣음 된다. 응? 왜 2로 나누나? 당근아니냐? 왼쪽 오른쪽 연장선 와서 굽힘점에서 만나니까~
절반만 구하면 되니까 2로 나누는 거고~ R은 반지름.... T는 두께이다... 응? 근데 여긴 두께가 별 필요가 없다.
왜? 이건 중심선에 대한 계산을 하기 때문에 두께가 없는 것이지.. 만약 중심선이 아닌 외경을 기준으로 한다면 말이 달라진다.
기본적으로 안쪽 반지름을 R이라 놓고 튜브의 지름을 T로 놓아서 결국 44로 계산하기 때문이지... 이건 Out side set back이고
안지름으로 T값 없이 하면 in side set back이 되겠지... 중심선도 마찬가지 T값은 없게 된다.
일단 C구간을 구하기 전에 D구간을 먼저 알아보자. 왜??
그래야 전체 120mm에서 B구간 빼고 D구간 빼면 당근으로 C구간이 나올테니까~~
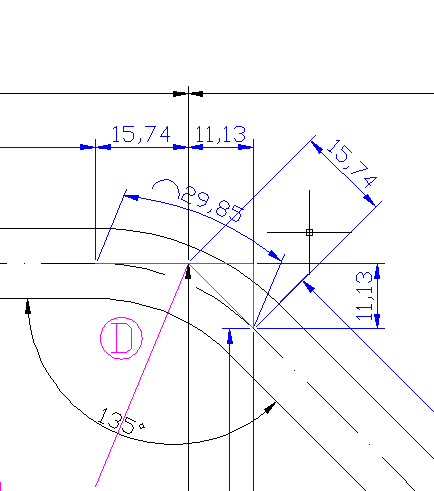
D구간은 어떻게 구해야 할까?
일단 SET BACK을 배웠으니 그걸로 하면 되겠지~ 근데 바보 같이 135도를 넣고 구하면 안된다.
요게 함정이지... 왜????? 135를 주었을까? 중심선이 C구간을 중심으로 아래쪽으로 굽혀졌을 때 135도라고 표시한게 맞기는 하다.
하지만 우리가 구해야할 것은 반대편의 각도 즉 180도에서 135도를 뺀 45도를 갖고 계산을 해야 한다는 것이다.
C구간에서 제군들이 구부려야 하는 각도가 바로 45도이기 때문이지.....
135라고 찍혀 있다고 아하~~ 하고 SET BACK에 가볍게 135도를 넣으면 시험 끝나고 쓰나미 같은 멘붕이 다가 올게다 ㅋㅋㅋㅋ
그림에 보면 핑크색의 연장선이 보일게야~ 그 선은 굴곡이 시작되는 부분에서의 연장선이다. 두 녀석이 겹치는 부분을 굽힘점이라고 하지.
그럼 두녀석의 길이를 각각 계산해 보자~ 아까 보여준 SET BACK 공식을 이용해서 풀어보면......
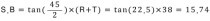
와우~~ 그림에 나온 것과 똑같네~ ㅎㅎㅎ 근데 이게 2개를 쪼개 놓은 것이니 둘다 15.74mm라는 수치가 나오는 것이겠지~
물론 그림은 계산해서 만든게 아니라 딱 45도 만큼 그렸기에 수치가 저렇게 딱 떨어지는 것임을 제군들은 알아야 할게야~~
자 그럼 오른쪽 15.74가 있는 곳의 핑크색 삼각형을 보자.. 이거 제길... 이제 피타고라스를 소환하자.
피타고라스~ 뭐... 별로 나랑 친하진 않지만... 녀석이 한말을 잘 곱씹어 보지 않고도... 검색창에 피타고라스의 정리~~ 라고 써주면 알아서
잘 까발려 줄게다.
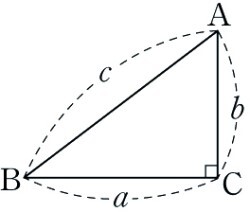
요것도 어디서 많이 봤지? 그래 피타고라스의 친구 직각삼각형이다. ㅋㅋㅋㅋ
피타고라스~~ 이거만 기억하자.. ㅋㅋ
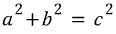
조낸 쉽지 않은가? 응?? 근데 제곱을 어떻게 제거 하냐구?? 아나.. 루트~~ 루트다...
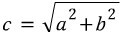
결국 대각선 C를 구할람 a의 제곱 + b의 제곱을 루트를 씌워버리면 되는 것이다.
근데... 위에 핑크색 선을 보면 말이다. 11.13이란 기럭지는 어떻게 나올까?
모르는 제군을 위해 함 씨부려 보겠다. ㅋㅋ
일단 핑크색 삼각형은 2등변 직각삼각형이다. 결론은 대각선인 빗변을 제외한 나머지 변은 길이가 같은 녀석이란 거지....
그럼 위의 피타고라스를 적용해서 빗변만 갖고 양변을 구할 수 있게 된다.
일단 두변이 같으니 제곱 + 제곱 = 15.74의 제곱이 되고, 제곱을 서로 더했으니 결국은 제곱이 두배가되는 거다. 이걸 루트를 이용해서 제곱을
샤샤삭 벗겨내면 말이다.
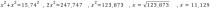
이렇게 얻어지는거지.... 설마 이런거 모른다고 발뺌하면 곤란하다. ㅋㅋㅋㅋ
이렇게 계산해 보면 굴곡이 있는 부분의 직선길이는 SET BACK의 길이와 11.129가 더해진 길이가 된다. 이렇게 하면 위쪽 총길이 410mm를 잘 맞추게 될게다.
아차....
이게 중요한게 아니지.... ㅋㅋㅋㅋ
친하지도 않은 피타고라스란 녀석 이야기 하다 삼천포로 갈 뻔했다. ㅋㅋㅋ
우리가 구하는게 뭐?? 그래... C구간이다. 이제 양쪽에 빼야할 길이를 알았으니 과감하게 빼보자.
120mm - B구간(44mm) - S.B(15.74mm) = 60.26mm
캬~~ 이거 완전 쉽지 않냐? 이해가 안간다구?? 그럼 내년은 언제 오는거냐?? ㅋㅋㅋㅋㅋㅋ
자... B구간 90도 구부리고 멈춘 부분에서 60.26mm 빼고 이제 45도를 구부리면 된다. 휴~~ 여기 까지 달리는 것도 손꾸락이 아프다 ㅋㅋㅋㅋ
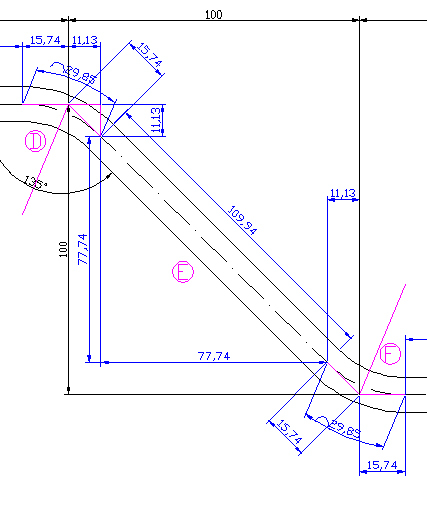
제군들 이제 E구간 오셨다 휴~~ 한숨 돌리고 달리기 시작하자.. ㅋㅋㅋㅋ
이제부턴 어려운 계산이 없다. 그냥 사칙연산만 잘하면 날로 먹는 구간이니 일단 안도의 한숨 먹어라~~ 휴~~~~~~ ㅋㅋ
일단 E구간이 존재하는 곳의 가로길이가 위에 껌정 글씨로 나왔다. 얼마인고???? 100mm 되시겠다.
근데 또 잔대가리 굴린다고 15.74의 제곱에 어쩌구 저쩌구 11.13을 양쪽으로 빼고 날라차기, 돌려차기, 옆차기 하지 말아라.
아까 말한 11.13은 그냥 그렇게 구한다~~ 라는 것을 보여주기 위함이다. 근데 여기선 그게 필요하게 된다. 왜? 피타고라스가 이때 쓰이는 거니까~
잘 보면 말이다. 가로 총길이는 100mm이다. 근데 세로에 검정글씨로 높이가 나오지? 그게 또 100mm이다. 응??
결국은 대각선 길이.... S.B + E구간 + S.B는 얼마인지 모르겠지만...... 밑변 100mm이고 높이 100mm인 이등변 직각삼각형이 그려진다.
근데 아까 피타고라스가 뭐라 했냐?
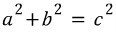
그래 정답이다. 아까 대각선 길이가 C라고 하지 않았는가? 결국은 C를 구할라면 A의 제곱 + B의 제곱에 루트를 살포시 씌워주면 되는거다.
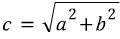
캬~ 그럼 어찌 계산해 볼까??
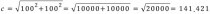
자.. 이 수치는 핑크색 연장선인 S.B을 포함한 거리이다. 더군다나 양쪽으로 더해져 있네 ㅋㅋ
그럼 141.421에서 15.74을 두번 빼주면 중간 길이가 딱 나오겠지???
C = 141.421 - 15.74 - 15.74 = 109.94mm
우와~~ 아주 쉽지 않은가? 아까 S.B를 구해 놓으니 아주 일사천리 뿅뿅뿅~~~ 대출 만큼 빠르게 풀리는 군화~~ 냐하하하하 ^^;;
이제 아까 구부린 부분의 끝에서 109.94mm를 띄고서 또 반대로 45도 구부려 주면 된다.
뭐 굳이 양쪽에 11.13을 구해서 난 77.74를 얻고나서 중간 길이 쏙 꺼내겠다~ 라는 생각도 좋다....
하지만 시험봐봐라 그럴 시간 뽀지게 남아도는지 ㅋㅋㅋ 그냥 닥치고 쉽고 빠른 방법이 장땡이다 ㅋㅋㅋ
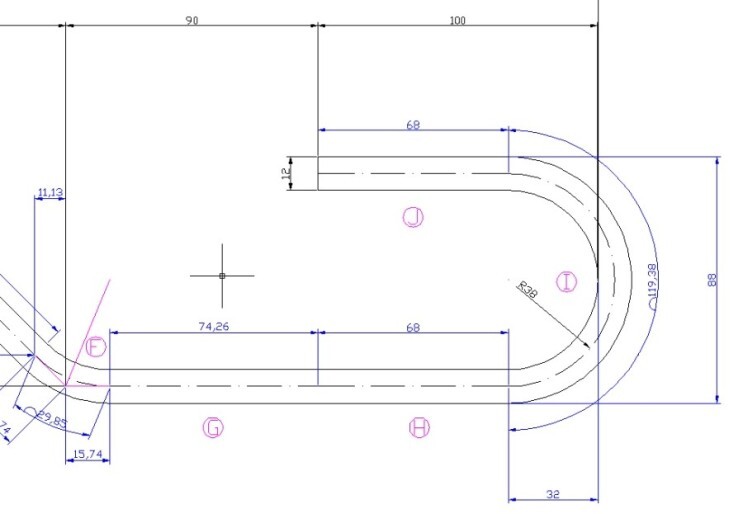
자.. 이제 거의 마지막에 다가왔다. 힘내자~~!!
뭐 F 구간은 따로 설명하지 않겠다. 왜??
아까 D구간 한거 뒤집어 놓은거니 다를게 없어서 이다 ㅋㅋㅋ 하지만 아까 구한 15.74는 여기서도 필요하다 ㅋㅋ
이번엔 G와 H를 동시에 나가보자. 두개를 구해서 빼 놓고 180도를 구부리면 되는 거니까~ ㅋㅋ
F부분에서 I부분까지의 길이는 검정글씨로 90mm와 100mm를 합친 190mm란다.
근데 I는 내경으로 길이를 구했군... 당근이지... 제군들이 쓸 Tool이 바로 32mm짤이기 때문이다. 근데 또 여기다 장난질 쳐서 반지름이 31.2라고 하는 도면도 있다.
신경쓰지 말자 31.2짤 Tool은 없다 ㅋㅋ 대부분 시험장엔 32mm짤이다 ㅋㅋㅋ
결국 32mm짤 기준으로 평가하게 되니까 말이다... I부분의 안쪽 반지름이 32mm란다. 100mm에서 32mm 가뿐히 빼주신다.
90mm짤에서는 S.B인 15.74를 빼주면 되시겠다.
G+H = 190 - 32 - 15.74 = 142.26mm 되시겠다.
142.26 mm 지나고나서 가뿐하게 180도 돌려 주어라~ 아주 쉽다. 못 돌리는게 웃기는 거다 ㅋㅋㅋ
여기서 J를 보자.. 왜? 68mm인가?
당근 아니냐? 100mm에서 I부분의 안지름 32mm를 빼냈지 않는가? 그러니 68mm가 되는거다.
그럼 H와 J는 같은 길이이니 H는 68mm가 되는거고, G구간은 142.26 - 68 = 74.26mm가 되는 것이다.
아따 한방에 훌쩍 뛰어 넘었네 ㅋㅋㅋ
이렇게 총길이 410mm를 맞추는 튜브 벤딩을 배워봤다.
물론 구부리는 기술은 자신들이 수평이 잘 맞게 구부리기 바란다. 난 제군들이 빠르게 계산해서 빠르게 구부리길 기대해본다.
마지막으로 전체 도면을 까발려 볼까 하다 말았다 ㅋㅋㅋ 뭐 어짜피 전체 도면이 조각나서 그림으로 올라왔으니 헷갈리지 않으리라 장담한다.
그리고 계산을 빨리하는 방법을 터득하는게 좋겠다. 제군들은 똑똑하니까 말이다 ㅋㅋ
그럼 이상 극악샒의 교육을 마친다... 오바~~ ㅋㅋ


